Data sources and study population
Our study utilized a customized database within healthcare big data provided by the National Health Insurance Service of Korea. The data included both outpatients and inpatients diagnosed with heatstroke according to the International Classification of Diseases, 10th Revision (ICD-10: T67) from 2011 to 2020. The study cities were Seoul, Busan, Daegu, Incheon, Gwangju, Daejeon, and Ulsan.
Table 1 shows the number of patients who suffered from heat-related illness (HRI). Over the 10-year period, 296,829 people were diagnosed with HRI. Of these, 46,393 were aged 65 or older and 250,436 were younger than 65. The dataset also included 13,735 disabled patients, categorized as 4,106 severely disabled and 9,629 mildly disabled. Low-income and outdoor workers were 51,653 and 33,159, respectively.
Table 1. Number of HRI patients used in the study (2011–2020).
Ethical approval
Our study protocol underwent thorough review and was approved by the Institutional Review Board (IRB) of Gongju National University (Confirmation No. 2022-46). Given the observational nature of this study and the utilization of anonymized statistical data, the IRB committee dispensed with the need for informed consent. All methodologies conformed to the guidelines for the use of health and medical data set forth by the Korean government.
Socio-economic classification
Participants were categorized into elderly, young, outdoor workers, low-income, and disabled groups based on socio-economic factors. Those aged 65 years or older were referred to as elderly, and those below this threshold as young. The outdoor workers category included professionals from various sectors, including agriculture, hunting, forestry, fishing, mining, electricity, construction, and manufacturing. The low-income group consisted of individuals who belonged to the lowest fifth of insurance and medical assistance recipients. Disability types, officially defined by the National Health Insurance Corporation, included physically disabled, brain-damaged, blind, other disabilities (language, intellectual, autistic, mental, kidney, heart, respiratory, liver, face, ostomy, urinary tract, epilepsy), and national achievement with related disabilities. Disability grades follow the Korean Disability Grading System and criteria for determining the degree of disability. Since 2019, Korea has been classified into severe (grades 1-3) and mild (grades 4-6).
Weather Data
Weather data were obtained from ASOS (Automatic Observation System) for each city provided by the Korea Meteorological Administration. Daily maximum temperature (Tmax) and daily average humidity were incorporated into the analysis.
Empirical Methodology
The statistical analysis is divided into two stages. In the first stage, we applied time series regression to each city to derive estimates of the location-specific association between heat stroke and ambient temperature, reported as relative risks (RRs). To analyze the relationship between heat stroke and ambient temperature, we adopted DLNM (distributed lag nonlinear model). DLNM has been widely used in epidemiology26,27,28,29. The main features of DLNM are nonlinearity, time-lagged effects, and control of confounders. This model allows us to capture nonlinear relationships between exposure and outcome variables. This model considers the lagged effect of exposure on the outcome. This model can incorporate adjustment for potential confounders or time-varying covariates. The variable configuration of the model in this study is as follows:
$${\text{ln}}{y}_{t}=\alpha +\beta \times Tma{x}_{t-3}+N{S}_{1}\left(s{n}_{t}\right)+N{S}_{2}\left(rhav{g}_{t}\right)+N{S}_{3}\left(do{y}_{t}\right)+\gamma \times weekda{y}_{t}+{\varepsilon }_{t},$$
where \({y}_{t}\) is the number of heat stroke cases, \(rhav{g}_{t}\) is the daily average humidity, \(do{y}_{t}\) is the number of days in a year, and \(s{n}_{t}\) is the serial number. The degrees of freedom for \(s{n}_{t}\) are set to 6 times the decade, which is the range of the data. \(weekda{y}_{t}\) are the days of the week. Natural cubic splines (NS) show the nonlinear relationship between the dependent and independent variables. Besides the time of day \(t\) variable, the daily maximum temperature \(Tma{x}_{t-3}\) is a 3-day time series. The use of lagged series is consistent with the work of Hess et al., Heo et al., and Royé et al., who provide evidence that the effects of heat waves remain strong over the period26,27,28.
Once the DLNM has been fitted, the estimated coefficients obtained from the model can be used to calculate relative risks. DLNM estimates a log-linear relationship between exposure and outcome, and the relative risks can be derived by exponentiating the coefficients associated with the exposure variables as follows:
β is the estimated coefficient from DLNM, which represents the log relative risk. Relative risk measures the incidence of cases above a certain temperature while holding all other confounding factors.
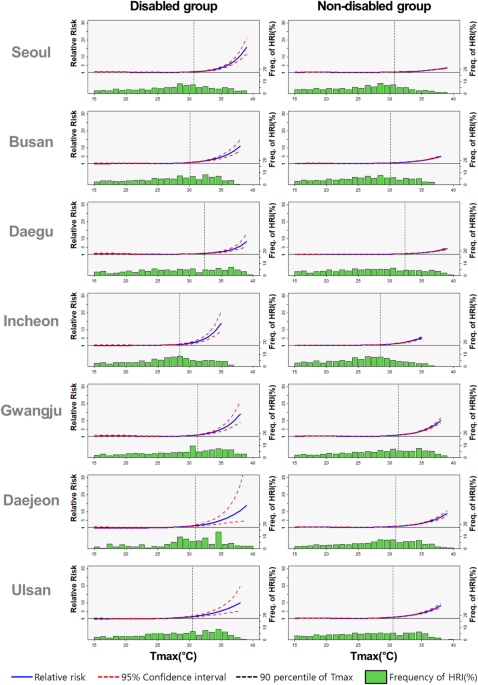
To compare relative risks between groups or cities, we converted the nonlinear RRs to average RRs above the 90th percentile daily maximum temperature. The daily maximum temperature at which case numbers start to increase, i.e. the threshold temperature, varies for each city depending on the location-specific temperature range. We found that the threshold temperature was approximately the same as the 90th percentile daily maximum temperature for each city (as can be seen in the results). Therefore, we expressed the nonlinear RRs as quantitative effect sizes to facilitate comparisons between cities or groups, and averaged the RRs above the 90th percentile daily maximum temperature to use as the heatwave effect size in the next step.
In the second stage, meta-analysis was applied to integrate and analyze information across multiple cities. In the meta-analysis, the RRs from the first stage were pooled to calculate a more accurate and comprehensive relative risk. The weights assigned to each effect size (meaning RRs above the 90th percentile Tmax in this study) from the location-specific time-series regression analysis reflected its contribution to the overall effect estimate. The weights of the effect sizes were determined by the inverse variance method in this study. In the meta-analysis, fixed-effect and random-effect models are employed to estimate the average effect. The fixed-effect model is for data with the characteristics of population homogeneity, and the random-effect model is for heterogeneity. The Q statistic and Higgins’ I2 are applied to test the homogeneity of the populations. The homogeneity test was conducted using the Q statistic and Higgins’ I2. Due to the limited number of cases in the meta-analysis, homogeneity was determined to be significant when the p-value of the Q test was less than 0.1 and the I2 was greater than 50% (Table 2).
Table 2. Results of homogeneity tests within each group.
First-stage regressions were performed in R software (version 4.1.2) using functions from the dlnm package (version 4.3.0). For the second-stage meta-analysis, the meta package in R (version 6.5.0) was used.